Ziua mondiala a numarului Pi. Puteti rezolva aceasta problema de logica?
Data de 14 martie 2016, scrisa in format american 3.14.16, formeaza numarul pi aproximat. El este o constanta matematica ce reprezinta raportul dintre circumferinta si diametrul cercului, egal cu 3,14159.
Aceasta potrivire are loc in luna martie, o data la o suta de ani. Luni este ziua numarului Pi aproximat de la 3,14159 la 3,1416. Pi are un numar infinit de zecimale dupa virgula, fiind un numar irational.
Cu ocazia acestei zile va propunem o problema de logica postata de publicatia The Guardian pe site-ul lor: demonstrati ca suprafata albastra si cea rosie au arii egale.
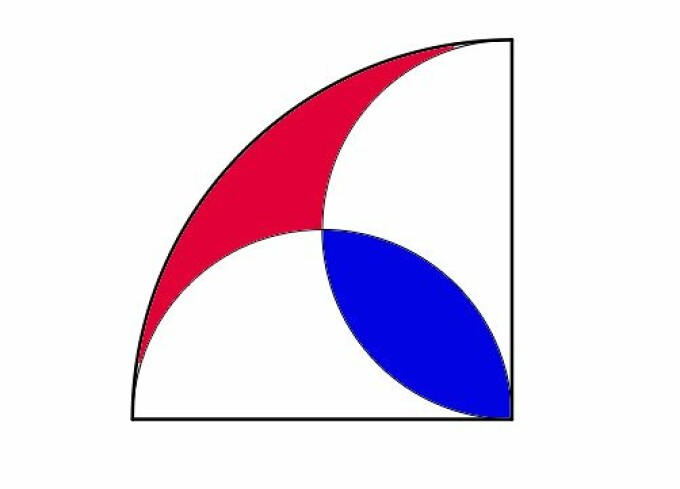
Solutie:
Se observa ca raza sfertului de cerc este dublul razei jumatatii de cerc inclusa in ea.
Aria cercului=pi*r*r
Aria sfertului de cerc mare=(pi*2r*2r)/4=(4*pi*r*r)/4=pi*r*r
Aria unei jumatati de cerc mic=(pi*r*r)/2
Cum aria sfertului de cerc mare este dublul ariei jumatatii de cerc mic, deci in ea ar intra exact doua semicercuri mici, rezulta ca aria in care cele doua se suprapun (cea albastra) este egala cu cea rosie.