O problemă de șah care i-a uimit pe matematicieni a fost rezolvată după mai bine de 150 de ani

Un matematician de la Harvard a rezolvat aproape integral o problemă de șah care datează de mai bine de 150 de ani.
Problema n-reginelor a început ca un puzzle mult mai simplu și a fost pusă pentru prima dată într-un număr din 1848 al ziarului german de șah Schachzeitung de șahistul Max Bezzel.
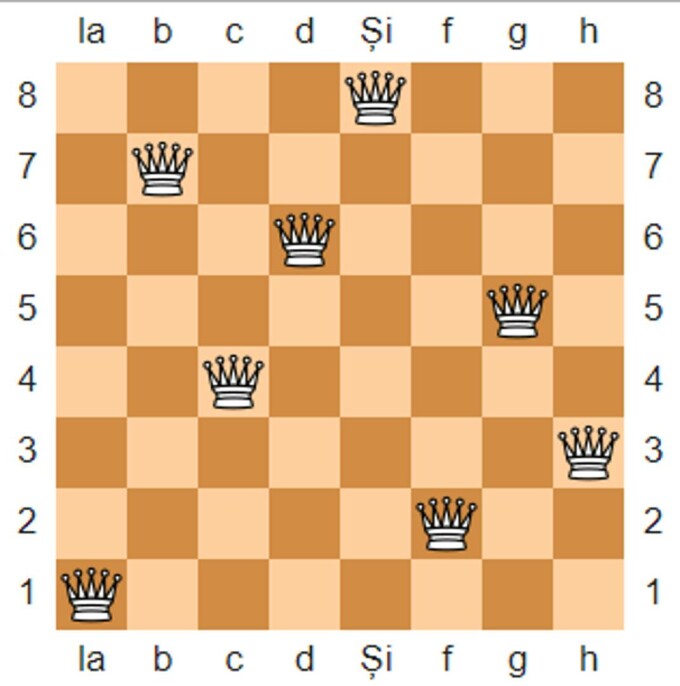
Bezzel a întrebat în câte moduri pot fi poziționate opt regine rivale – care sunt cele mai puternice piese de pe tabla de șah și capabile să se miște orice număr de pătrate pe orizontală, verticală și diagonală – pe o tablă standard de 64 de pătrate, fără ca vreo regină să atace pe alta, scrie Live Science.
Răspunsul, dezvăluit doar doi ani mai târziu, a fost că există 92 de configurații care țineau cele opt regine departe una de gâtul celeilalte, toate soluțiile, cu excepția a 12, fiind simple rotații și reflexii.
Dar, în 1869, matematicianul Franz Nauck complicat problema: în loc să configurați opt dame pe o tablă standard de 8 pe 8, ce zici de 1.000 de regine pe o tablă de 1.000 pe 1.000? Dar un milion, sau chiar un miliard?
Numărul de combinații: 1 urmat de 5 milioane de zerouri
Ceea ce era odată un puzzle relativ simplu devenise o problemă de matematică mult mai profundă – una care necesita descoperirea unei reguli generale pentru numărul de moduri de a poziționa orice număr (reprezentat ca „n”) de regine pe o tablă n-cu-n.
Acum, Michael Simkin, un matematician la Centrul de Științe și Aplicații Matematice al Universității Harvard, a venit cu un răspuns aproape definitiv.
Pe o tablă enormă n-cu-n, există aproximativ (0,143n)^n moduri de a plasa n regine, astfel încât niciuna să nu o poată ataca pe cealaltă.
Asta înseamnă că pe o tablă de milion cu un milion, numărul de configurații neamenințătoare în care pot fi aranjate 1 milion de regine este de aproximativ 1 urmat de 5 milioane de zerouri.
Simkin a avut nevoie de aproape cinci ani pentru a găsi această aproximare apropiată a unei ecuații. De obicei, matematicienii rezolvă probleme găsind modalități de a le împărți în bucăți mai ușor de gestionat.
Dar pentru că reginele plasate mai aproape de centrul unei table pot ataca mult mai multe pătrate decât pot ataca reginele de la margini, problema n-reginelor este foarte asimetrică – și, prin urmare, rezista cu încăpățânare la orice tentativă de simplificare.
A fost inventată strategia ”algoritmului lacom aleatoriu”
Colaborând cu Zur Luria, un matematician la Institutul Federal Elvețian de Tehnologie din Zurich, Simkin a simplificat inițial sarcina luând în considerare o versiune „toroidală” mai simetrică a problemei, în care pătratele de margine se înfășoară în jurul tablei. Acest aranjament permite reginelor să dispară în stânga sus și să reapară în dreapta jos, de exemplu.
De asemenea, înseamnă că indiferent unde sunt plasate, fiecare regină poate ataca același număr de pătrate ca și omoloagele sale.
Folosind placa toroidală ca primă aproximare, cei doi matematicieni au aplicat în continuare problemei o strategie numită „algoritm lacom aleatoriu”.
Au plasat o regină la întâmplare, blocând toate pătratele pe care le ataca; apoi următoarea regină va fi aleasă să stea pe locurile rămase, cu pătratele sale de atac blocate pe rând.
Perechea a continuat să facă acest lucru în mai multe configurații până când au găsit o limită inferioară aproximativă - sau cel mai mic număr posibil - pe numărul de configurații de n dame pe o placă toroidală.
Natura înfășurată a tablei ridică alte probleme
Dar estimarea lor era departe de a fi perfectă. Natura înfășurată a tablei i-a împiedicat să găsească ultimele poziții în unele configurații.
După ce a renunțat la problemă timp de câțiva ani, duo-ul s-a întors la ea cu ideea de a-și adapta algoritmul la o placă obișnuită, care a oferit mai multe locuri de ascunzătoare pentru reginele finale decât placa toroidală.
Prin adaptarea algoritmului lacom aleatoriu la o placă standard, non-toroidală, perechea a îmbunătățit oarecum precizia acestei estimări inferioare.
Dar răspunsul lor nu a fost atât de clar pe cât sperau – algoritmul lacom aleatoriu funcționează cel mai bine în problemele simetrice, în care fiecare pătrat oferă același avantaj de atac ca oricare altul.
Acesta nu este cazul unei table standard, în care pătratele de margine au o capacitate de atac mult mai mică decât pătratele din centru.
”Am terminat cu problema n-reginelor pentru o perioadă”
Pentru a rezolva această problemă, Simkin și-a dat seama că va trebui să adapteze algoritmul. Deoarece majoritatea configurațiilor viabile de pe o tablă standard aveau mai multe dame la marginile tablei - unde atacau mai puține pătrate - decât în centrul acesteia, Simkin a rafinat algoritmul lacom aleatoriu ponderând pătratele.
În loc ca algoritmul său să atribuie regine la întâmplare, a plasat de preferință damele în locuri care s-ar ramifica la cel mai mare număr de configurații posibile.
Acest lucru i-a permis lui Simkin să se concentreze pe câte regine ar ocupa fiecare secțiune de tablă și să găsească o formulă pentru un număr valid de configurații, îmbunătățind astfel acuratețea ipotezei limitei inferioare și mai mult.
Lucrările viitoare ar putea încerca să strângă și mai mult cele două limite, dar Simkin, după ce s-a apropiat mai mult decât oricine înaintea lui, se mulțumește să lase această provocare pentru ca altcineva să o cucerească.
„Cred că personal am terminat cu problema n-reginelor pentru o vreme”, a spus Simkin. „Nu pentru că nu mai are nimic de-a face cu asta, ci doar pentru că am visat la șah și sunt gata să merg mai departe cu viața mea”.